Школьная олимпиада по математике 9 класс.
Вариант 1
1. Постройте треугольник по стороне, противолежащему углу и медиане, проведенной к другой стороне (исследование вопроса о количестве решений не требуется).
2. В выпуклом четырехугольнике ABCD ÐABC= 900, Ð BAC = Ð CAD, AC = AD, DH — высота треугольника ACD. В каком отношении прямая BH делит отрезок CD?
3. Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС. На окружностях (в одной полуплоскости относительно АС) выбраны соответственно точки M и L так, что Ð MBA = Ð LBC. Точки K и F отмечены соответственно на лучах ВМ и BL так, что BK = BC и BF = AB. Докажите, что точки M, K, F и L лежат на одной окружности.
4. В треугольнике ABC M — точка пересечения медиан, O — центр вписанной окружности, A', B', C' — точки ее касания со сторонами BC, CA, AB соответственно. Докажите, что, если CA' = AB, то прямые OM и AB перпендикулярны.
5. Дан треугольник АВС. Точка О1 — центр прямоугольника ВСDE, построенного так, что сторона DE прямоугольника содержит вершину А треугольника. Точки О2 и О3 являются центрами прямоугольников, построенных аналогичным образом на сторонах АС и АВ соответственно. Докажите, что прямые АО1, ВО2 и СО3 пересекаются в одной точке.
6. На плоскости расположен круг. Какое наименьшее количество прямых надо провести, чтобы, симметрично отражая данный круг относительно этих прямых (в любом порядке конечное количество раз), можно было накрыть им любую заданную точку плоскости?
Школьная олимпиада по математике 9 класс.
Вариант 2
1. В выпуклом четырехугольнике АВСD Е – середина CD, F – середина АD, K – точка пересечения АС и ВЕ. Докажите, что площадь треугольника BKF в два раза меньше площади треугольника АВС.
2. Постройте треугольник АВС по углу А и медианам, проведенным из вершин В и С.
3. Дан квадрат ABCD. Найдите геометрическое место точек M таких, что Ð AMB = Ð CMD.
4. Треугольник ABC вписан в окружность. Через точки A и B проведены касательные к этой окружности, которые пересекаются в точке p. Точки X и Y – ортогональные проекции точки p на прямые AC и BC. Докажите, что прямая XY перпендикулярна медиане треугольника ABC, проведенной из вершины C.
5. Диагонали вписанного четырёхугольника ABCD пересекаются в точке M, Ð AMB = 60° . На сторонах AD и BC во внешнюю сторону построены равносторонние треугольники ADK и BCL. Прямая KL пересекает описанную около ABCD окружность в точках p и Q. Докажите, что pK = LQ.
6. Длина каждой стороны и каждой не главной диагонали выпуклого шестиугольника не превосходит 1. Докажите, что в этом шестиугольнике найдется главная диагональ, длина которой не превосходит 2 деленное на корень из 3.
Школьная олимпиада по математике 9 класс.
Вариант 3
1. На рисунке изображен параллелограмм и отмечена точка p пересечения его диагоналей. Проведите через p прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.
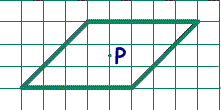
2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.
3. В треугольнике АВС АА1 и ВВ1 — высоты. На стороне АВ выбраны точки М и К так, что В1К || BC и А1М || АС. Д окажите, что угол АА1К равен углу ВВ1М.
4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)
5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?
6. Фиксированы две окружности w1 и w2, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w1 и w2 соответственно, а треугольник XYZ содержит окружности w1 и w2. Докажите, что центры окружностей, вписанных в треугольники XYZ, лежат на одной прямой.


