В клетках шахматной доски стоят натуральные числа так, что каждое равно среднему арифметическому своих соседей.
Сумма чисел, стоящих в углах доски, равна 16.
Найдите число, стоящее на поле e2.
Задача 2.
Решите следующий числовой ребус:

Здесь цифры заменены буквами и звёздочками.
Одинаковыми буквами заменены одинаковые цифры, а разными буквами — неодинаковые цифры; звёздочки же поставлены взамен любых цифр, как одинаковых, так и неодинаковых.
Задача 3.
Этот ребус усложнён тем, что не известно даже число цифр делителя, и всё же ребус имеет единственное решение:
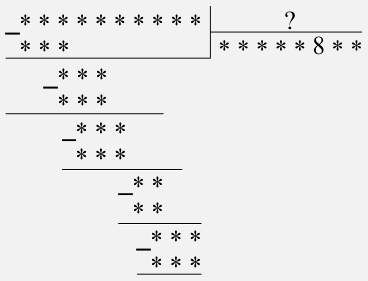
Задача 4.
Решите следующий числовой ребус:
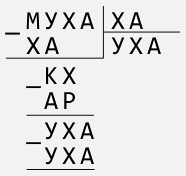
Здесь цифры заменены буквами, причём одинаковыми буквами заменены одинаковые цифры, а разными буквами — неодинаковые цифры.
Задача 5.
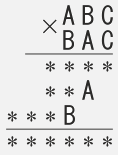
Восстановите этот пример умножения, подставив вместо звёздочек подходящие цифры:

Задача имеет единственное решение.
Задача 6.
Решите следующий числовой ребус:
Здесь цифры заменены буквами и звёздочками. Одинаковыми буквами заменены одинаковые цифры, а разными буквами — неодинаковые цифры; звёздочки же поставлены взамен любых цифр, как одинаковых, так и неодинаковых.
Задача 7.
Найдите первые 1963 цифры после запятой в десятичной записи числа
Задача 8.
Некоторое натуральное число A делят с остатком на все натуральные числа, меньшие A.
Сумма всех различных остатков оказалась равна A.
Найдите A.
Задача 9.
В автобусе без кондуктора едут 40 пассажиров, имеющих при себе только монеты достоинством в 10, 15 и 20 копеек.
Всего при у пассажиров 49 монет.
Докажите, что пассажиры не смогут уплатить требуемое количество денег в кассу и правильно рассчитаться между собой (стоимость автобусного билета составляет 5 копеек).
Задача 10.
Возраст человека в 1962 году был на единицу больше суммы цифр года его рождения.
Сколько ему лет?
Задача 11.
Найти n + 1 последовательных чисел, сумма квадратов которых равна сумме квадратов следующих n чисел.
Задача 12.
При помощи десяти различных цифр можно составить шесть таких дробей, что каждая из них будет равна 9.
Три дроби таковы:
9 = 97 524 / 10 836 = 95 823 / 10 647 = 57 429 / 06 381
Найдите остальные три.
Задача 13.
Если одна цифра 2, употреблённая не более 5 раз, или одна цифра 4, употреблённая не более четырёх раз, в состоянии заменить собой любую из цифр от 1 до 9, то и вся эта дружная семья цифр не останется в долгу.
Участвуя всей семьёй сразу (но без нуля), они могут заменить собой любую цифру своего же семейства.
Вот так, например, они заменяют 2 и 4:
2 = 13 458 / 6729
4 = 15 768 / 3942
Каждая из этих неправильных дробей содержит все цифры от 1 до 9, причём каждую только по одному разу.
Составляя аналогичные дроби из тех же цифр и употребляя каждую цифру только по одному разу, вы можете образовать числа 3, 5, 6, 7, 8 и 9, то есть все остальные однозначные числа, кроме 1.
Для изображения 1 посредством девяти цифр надо придумать особый способ.
Задача 14.
Обобщим предыдущую задачу.
Изобразить целое число при помощи ровно четырёх любых одинаковых цифр, соединяя их математическими знаками. Это значит: изобразить число четырьмя цифрами так, чтобы при замене этих цифр четвёркой любых других одинаковых цифр (кроме нуля) получилось то же число. Например:
3 = (n + n + n) : n
При этом разрешается употреблять знаки сложения, вычитания, умножения и деления, скобки. Если этих знаков окажется недостаточно, то ещё
- знак квадратного радикала: v ;
- знак факториала: ! (этот знак ставится справа от числа и обозначает произведение всех натуральных чисел от 1 до этого числа включительно; например 5! = 1 ? 2 ? 3 ? 4 ? 5 = 120)
- точку перед числом (на уровне строки), например .4 (так иногда обозначают десятичную дробь: .4 = 0,4);
- точку перед числом и над числом, например .4? (так иногда обозначают периодическую дробь: .4? = 0,(4) = 4/9)
Известны решения этой задачи для любых целых чисел от 1 до 21, кроме 14.
Задача 15.
Изобразите все целые числа от 1 до 10 с помощью четырёх цифр 4.
Задача 16.
Запишите каждое из чисел от 1 до 26 с помощью только пяти двоек, пользуясь для этого четырьмя арифметическими действиями, возведением в квадрат и скобками.
Примечание: Изобразить число 27 пятью двойками при таких условиях не получится.
Задача 17.
Следующие две задачи надо решить с помощью «чистых» рассуждений, без использования уравнений.
1. Если некоторое двузначное число прочесть справа налево, то полученное «обращённое» число будет в 4,5 раза больше данного.
Что это за число?
2. Произведение четырёх последовательных целых чисел равно 3024.
Найти эти числа.
Задача 18.
Следующие две задачи надо решить рассуждением «от противного»:
1. Произведение двух целых чисел больше 75. Доказать, что хотя бы один из сомножителей больше 8.
2. Произведение некоторого двузначного числа на 5 — тоже двузначное число.
Доказать, что первая цифра данного множимого есть 1.
Задача 19.
Если от каждого из двух чисел отнять половину меньшего из них, то остаток от большего будет втрое больше остатка от меньшего.
Во сколько раз большее число больше меньшего?
Задача 20.
Записать число 100, используя по разу каждую из цифр 1, 2, 3, 4, 5.
Порядок цифр изменять не разрешается.
